DFA-AP

数据流分析总揽

数据流分析的核心：How Data Flows on CFG?

将这句话展开来，所谓数据流分析就是：

How application-specific Data (对数据的抽象：+, -, 0 等……)

Flows (根据分析的类型，做出合适的估算) through the

Nodes (数据如何 transfer, 如 + op + = +) and

Edges (控制流如何处理，例如两个控制流汇入一个BB) of

CFG (整个程序) ?

不同的数据流分析，有着不同的data abstraction, flow safe-approximation策略，transfer functions&control-flow handlings。

may analysis ：outputs information that may be true(over-approximation)

May analysis 关注程序中可能发生的行为，即分析的结果是程序中所有可能会发生的情况的上界，输出结果可能为真，可能引入假阳性（实际未发生也被标记为可能）

must analysis:outputs information that must be true(under-approximation)

Must analysis 关注程序中一定会发生的行为，即分析的结果是程序所有行为的下界，输出结果必须为真，可能引入假阴性（漏掉实际发生的情况）

Over- and under-approximations are both for safety of analysis.

Over-approximation（May Analysis）：为了避免遗漏潜在的危险行为，may analysis 通常牺牲精确性来涵盖所有可能性。这在安全性分析中非常重要，因为任何可能的漏洞都不能被忽略。

Under-approximation（Must Analysis）：强调分析结果的可信度和可靠性，即分析所证明的属性一定是真实的。这对验证某些安全性条件是否始终满足非常关键。

数据流分析的初步准备

1.Input and Output States 输入输出状态

• 每一条IR的执行，都会使状态从输入状态变成新的输出状态
• 输入/输出状态与语句前/后的 program point 相关联。

2.关于转移方程约束的概念

分析数据流有前向和后向两种

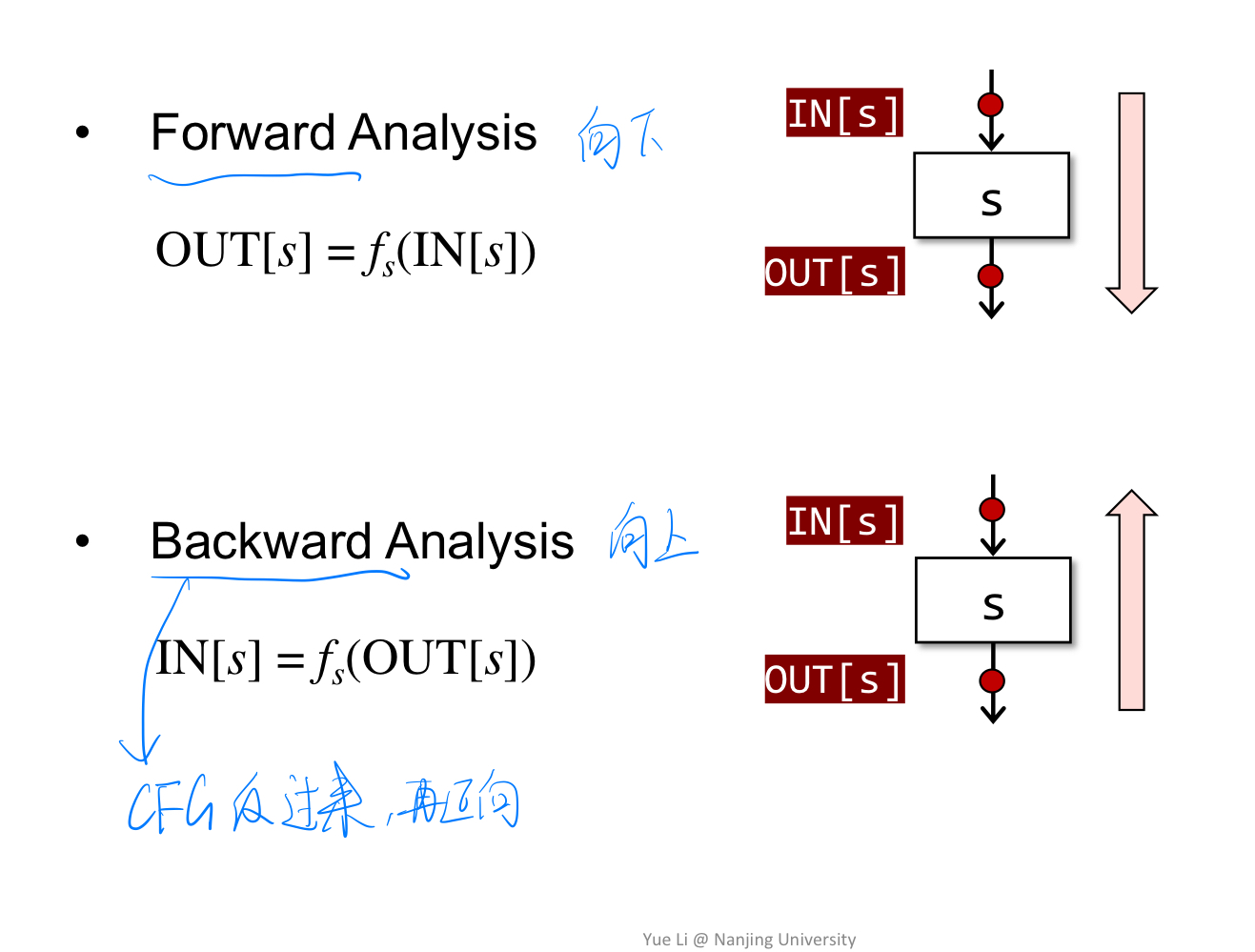
3.不会涉及到的概念

• 函数调用 Method Calls
  • 我们将分析的是过程本身中的事情，即 Intra-procedural。而过程之间的分析，将在 Inter-procedural Analysis 中介绍
• 变量别名 Aliases
  • 变量不能有别名。有关问题将在指针分析中介绍。

Reaching Definitions Analysis 到达定值分析

定义

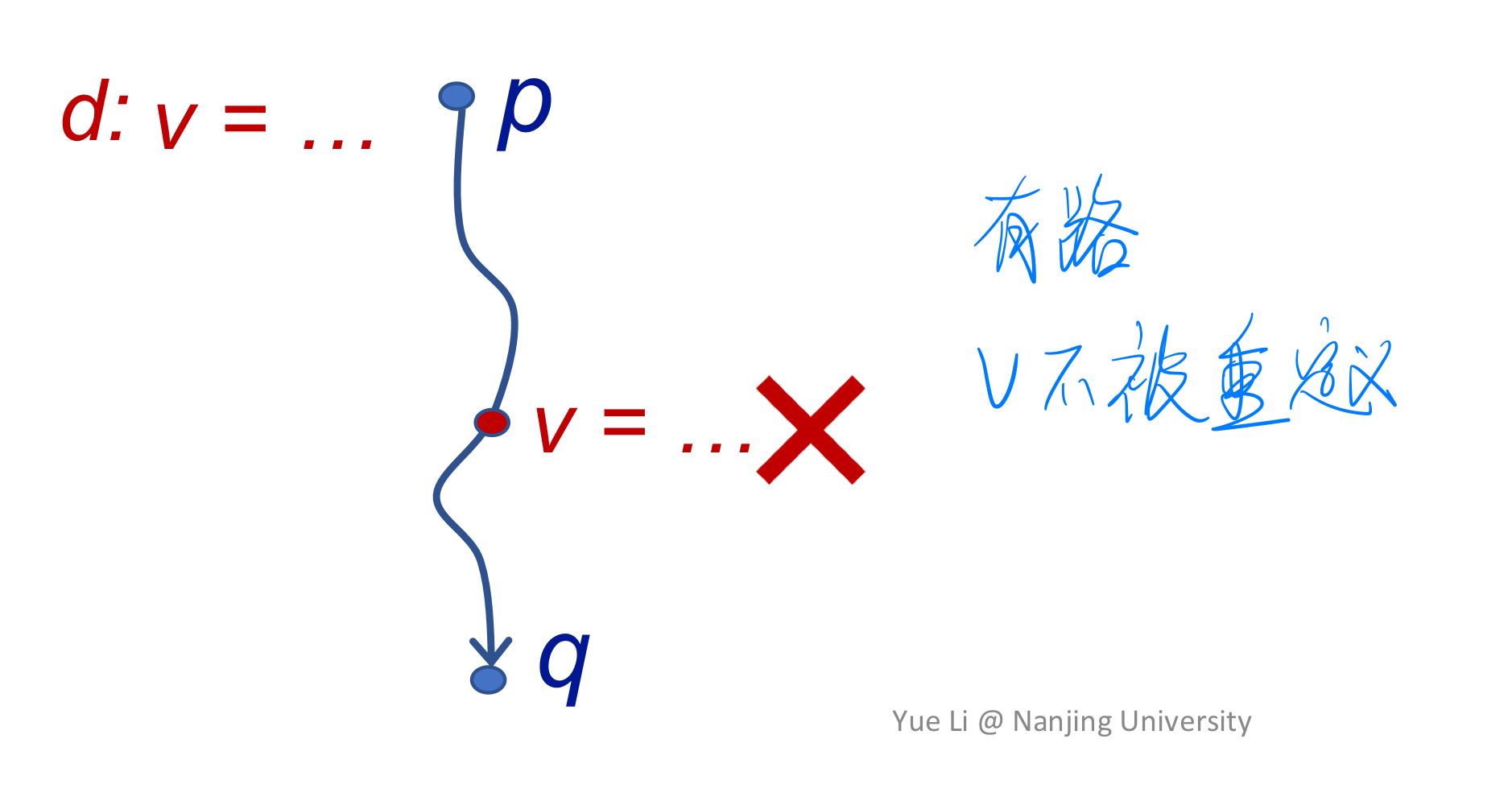
Reaching Definitions：A definition d at program point p reaches a point q if there is a path from p to q such that d is not "killed" along that path.

定义（许畅-编译原理）：假定 x 有定值 d (definition)，如果存在一个路径，从紧随 d 的点到达某点 p，并且此路径上面没有 x 的其他定值点，则称 x 的定值 d 到达 (reaching) p。如果在这条路径上有对 x 的其它定值，我们说变量 x 的这个定值 d 被杀死 (killed) 了

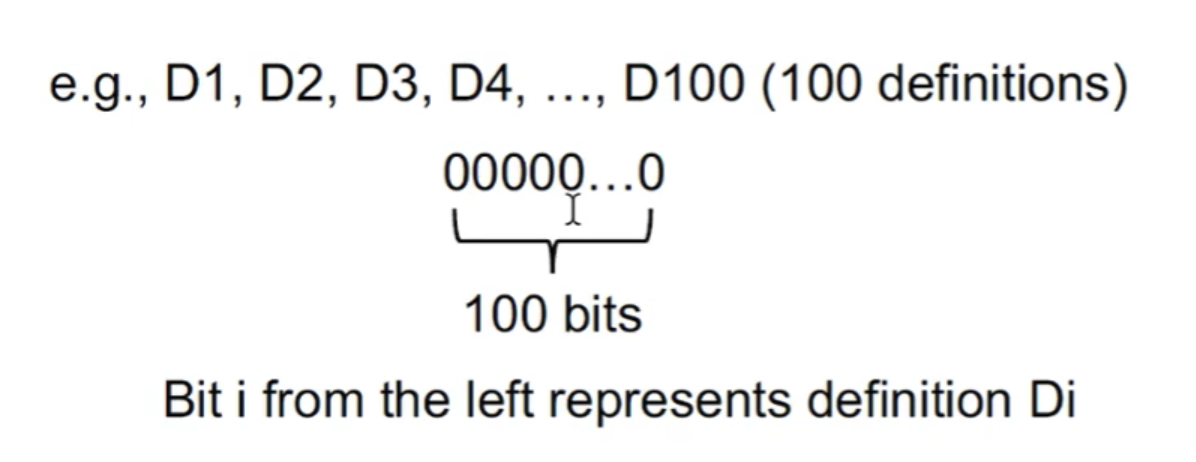
到达定值中的数据流值

• 程序中所有变量的定值。
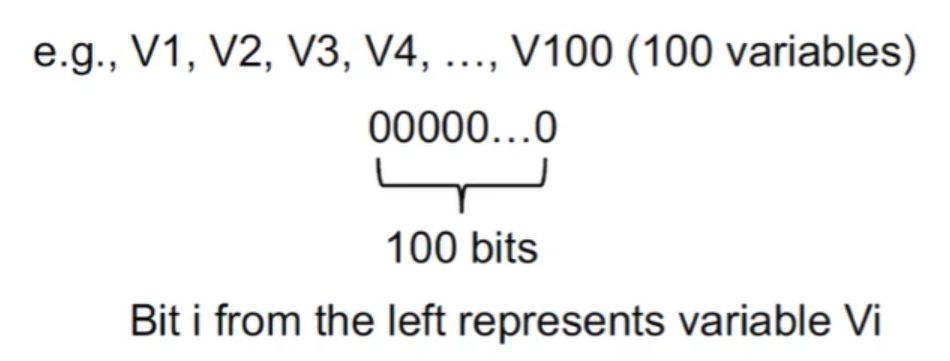
• 可以用一个 bit vector 来定义，有多少个赋值语句，就有多少个位。

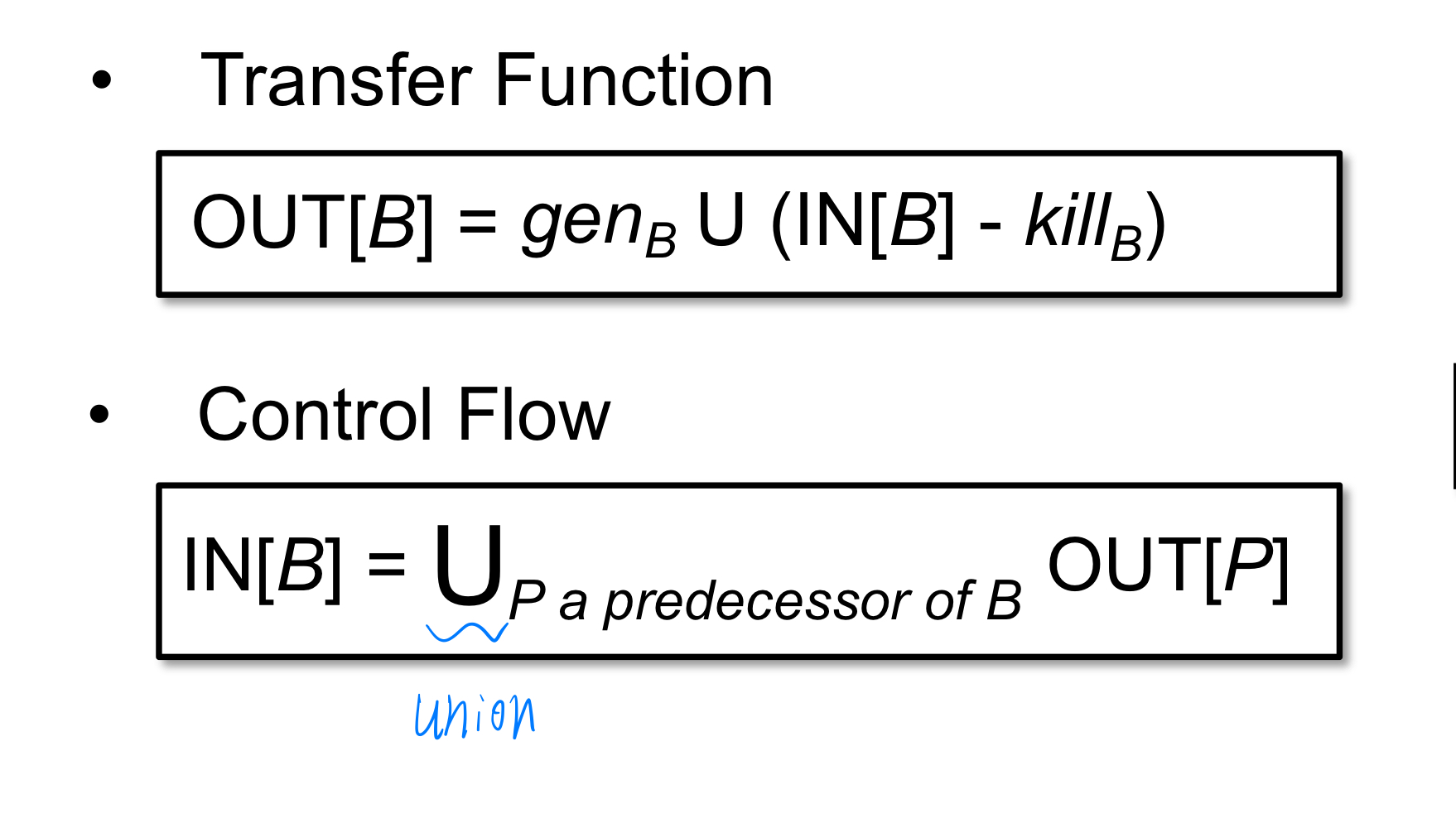
到达定值的转移方程和控制流处理

That statement "generates" a definition D of variable v and "kills" a;; the other definitions in the program that define variable v, while leaving the remaining incoming definitions unaffected.

语句 S 对变量 v 创建了一个新定义 D（即该语句定义了 v）。该定义 D 会取代程序中所有对 v 的旧定义，这些旧定义在 S 执行后变得无效（被“杀死”）。但是，程序中与变量 v 无关的其他变量的定义不会受影响，仍然保留原样。

Transfer function:从入口状态删除 kill 掉的定值，并加入新生成的定值；v = x op y，gen v, kill 其它所有的 v

control flow:任何一个前驱的变量定值都表明，该变量得到了定义。

到达定值算法

到达定值算法

这是一个经典的迭代算法。

• 首先让所有BB和入口的OUT为空。因为你不知道 BB 中有哪些定值被生成。
• 当任意 OUT 发生变化，则分析出的定值可能需要继续往下流动，所需要修改各 BB 的 IN 和 OUT。
• 先处理 IN，然后再根据转移完成更新 OUT。
• 在 gen U (IN - kill) 中，kill 与 gen 相关的 bit 不会因为 IN 的改变而发生改变，而其它 bit 又是通过对前驱 OUT 取并得到的，因此其它 bit 不会发生 0 -> 1 的情况。所以，OUT 是不断增长的，而且有上界，因此算法最后必然会停止。
• 因为 OUT 没有变化，不会导致任何的 IN 发生变化，因此 OUT 不变可以作为终止条件。我们称之为程序到达了不动点（Fixed Point）
• union为并集的意思，即有1为1，全0为0。
• 计算抽象说明就是在in上将gen的改为1，将kill的改为0。

到达定值算法例子1

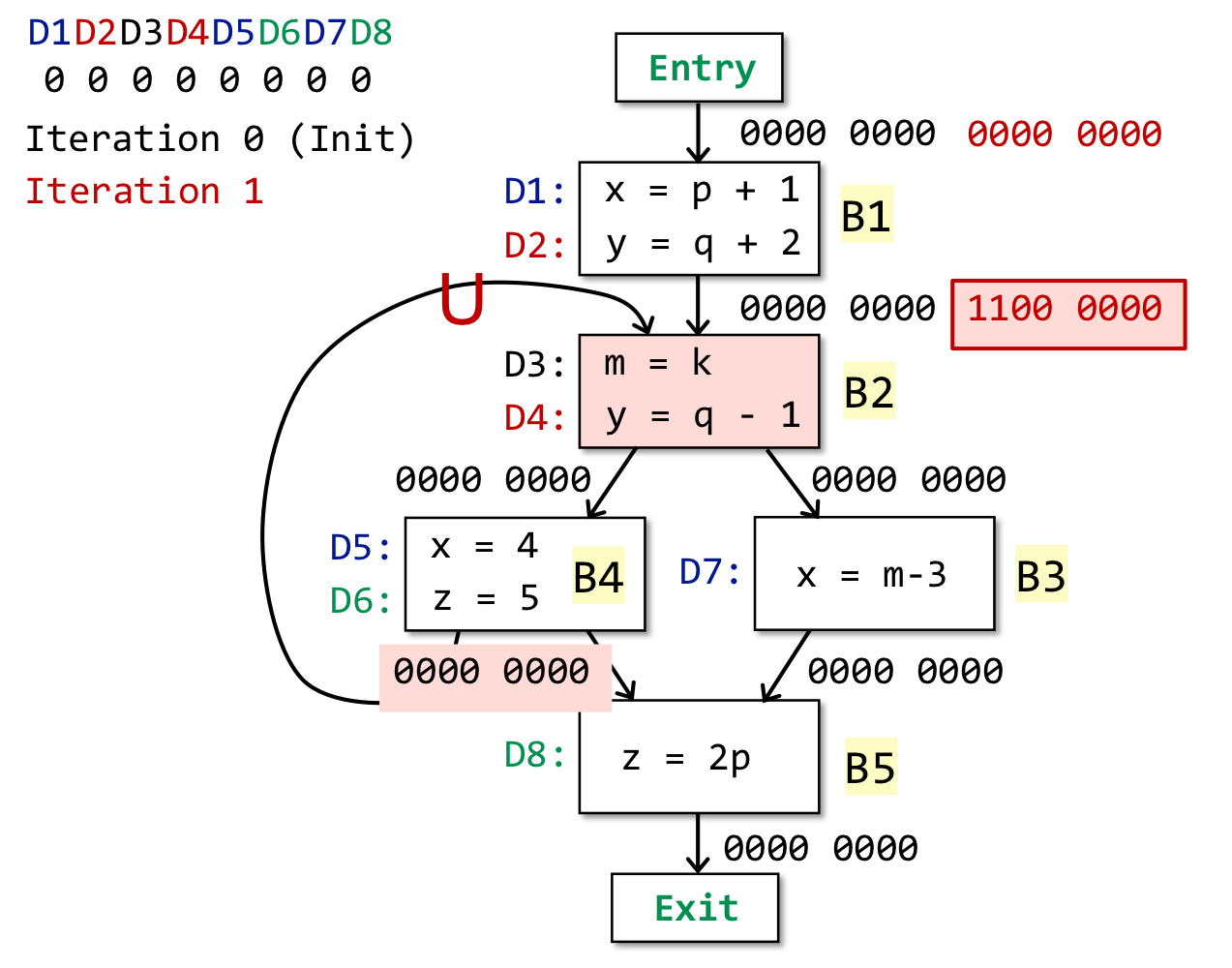
说明：初始定义所有BB的out为全0，之后从上至下依次根据公式更新。此时分析B2的out，注意到B2的in为B1的out和B4的out的union，故要先做union在继续分析B2的out。此时B2的in为11000000 U 00000000 = 11000000，gen为B2自身涉及的D3、D4即00110000，kill为之前涉及的D2（y）即01000000，故结果为00110000 U (11000000-01000000) = 10110000。

到达定值算法例子2

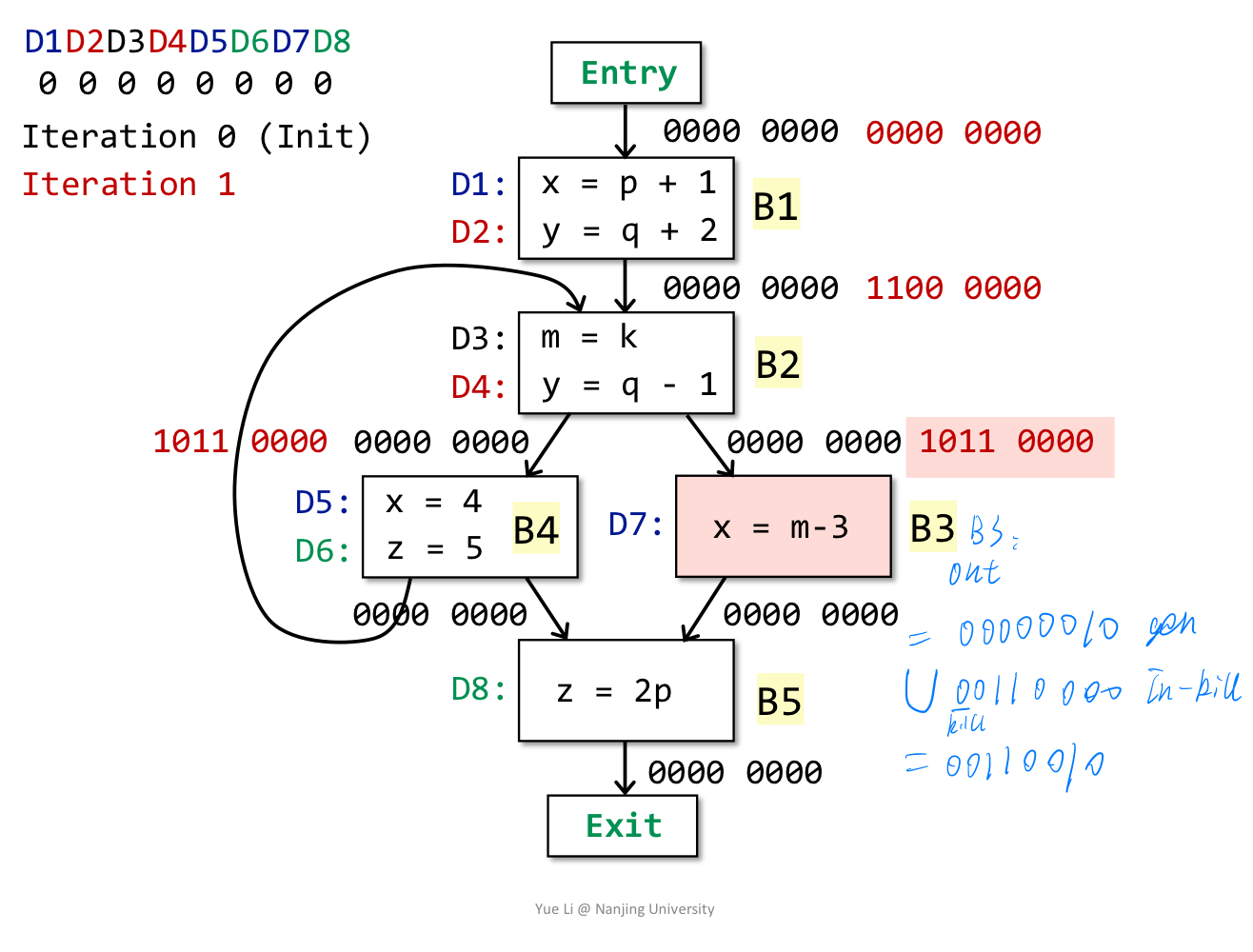
说明：此时分析B3的out，in为B2的out即10110000，gen为B3自身涉及的D7即00000010，kill为B3涉及到之前的D1（x）即10000000，故结果为00000010 U (10110000-10000000) = 00110010。

到达定值算法例子3

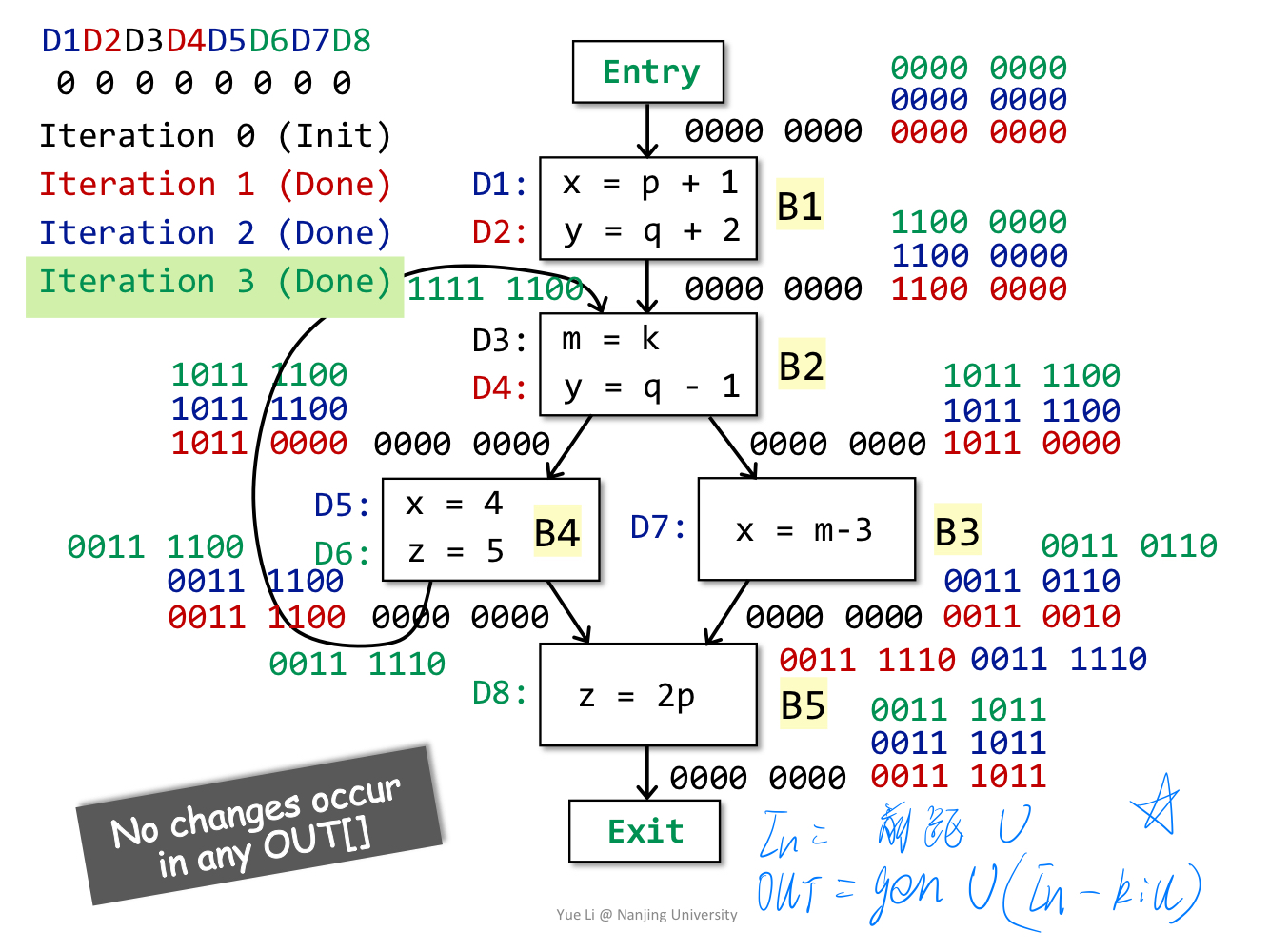
说明：经过3轮迭代计算，所有BB的out没有改变，此时到达不动点，算法结束。

到达定值算法最终会停原因

算法一定会停原因

单调性：OUT[S] 不会缩减

• 每次迭代时：
  • 和 是固定不变的。
  • 只会因为新增的 或 增加新的事实，但不会减少已有事实。
  • 因此， 是一个单调增长的集合。

有限性：事实集合大小有限

• 程序中的所有变量定义是有限的，因此整个程序中的事实集合是有限的。
• 不可能无限增加，因为程序中事实总数是有限的。

收敛性：新增事实最终停止

• 当所有 在某次迭代中不再有新事实加入时（即不再有新增的 或 ），算法达到收敛。
• 由于 永不缩减且集合有限，算法总会收敛到一个固定点（即最终的结果）。

Live Variables Analysis 活跃变量分析

定义

Live variables analysis tells whether the value of variable v at program point p could be used along some path in CFG starting at p. If so, v is live at p;otherwise, v is dead at p.

• 变量 x 在程序点 p 上的值是否会在某条从 p 出发的路径中使用。
• 变量 x 在 p 上活跃，当 且仅存在一条从 p 开始的路径，该路径的末端使用了 x，且路径上没有对 x进行覆盖。
• 隐藏了这样一个含义：在被使用前，v 没有被重新定义过，即没有被 kill 过。

这个算法可以用于寄存器分配，当一个变量不会再被使用，那么此变量就可以从寄存器中腾空，用于新值的存储。

使用backward后向分析来处理活跃变量分析更方便

活跃变量中的数据流值

• 程序中的所有变量
• 依然可以用 bit vector 来表示，每个 bit 代表一个变量

活跃变量的转移方程和控制流处理

活跃变量分析转移方程和控制流处理

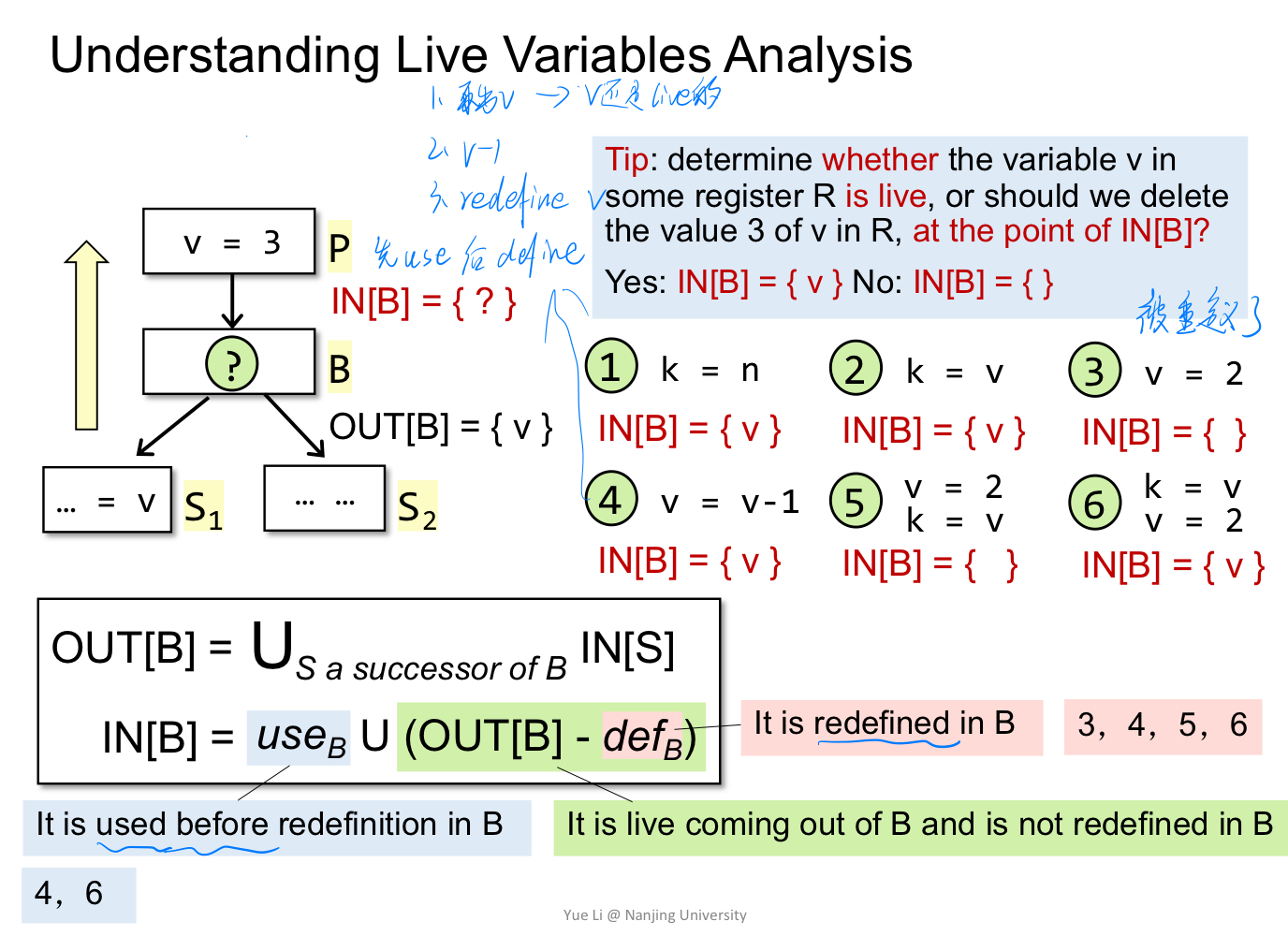
• 一个基本块内，若 v = exp, 则 def v。若 exp = exp op v，那么 use v。一个变量要么是 use，要么是 def，根据 def 和 use 的先后顺序来决定。
• 考虑基本块 B 及其后继 S。若 S 中，变量 v 被使用，那么我们就把 v 放到 S 的 IN 中，交给 B 来分析。
• 因此对于活跃变量分析，其控制流处理是 OUT[B] = IN[S]。
• 在一个块中，若变量 v 被使用，那么我们需要添加到我们的 IN 里。而如果 v 被定义，那么在其之上的语句中，v 都是一个非活跃变量，因为没有语句再需要使用它。
• 因此对于转移方程，IN 是从 OUT 中删去重新定值的变量，然后并上使用过的变量。需要注意，如果同一个块中，变量 v 的 def 先于 use ，那么实际上效果和没有 use 是一样的。
• 注意use和def的顺序，如图中的4和6。

活跃变量算法

活跃变量算法

• 我们不知道块中有哪些活跃变量，而且我们的目标是知道在一个块开始时哪些变量活跃，因此把 IN 初始化为空。
• 计算过程类似上文到达定值算法。
• 初始化的判断技巧：may analysis 是空（全0），must analysis 是 top（全1）。
• 计算抽象说明就是在out上将use的改为1，def的改为0。

活跃变量算法例子1

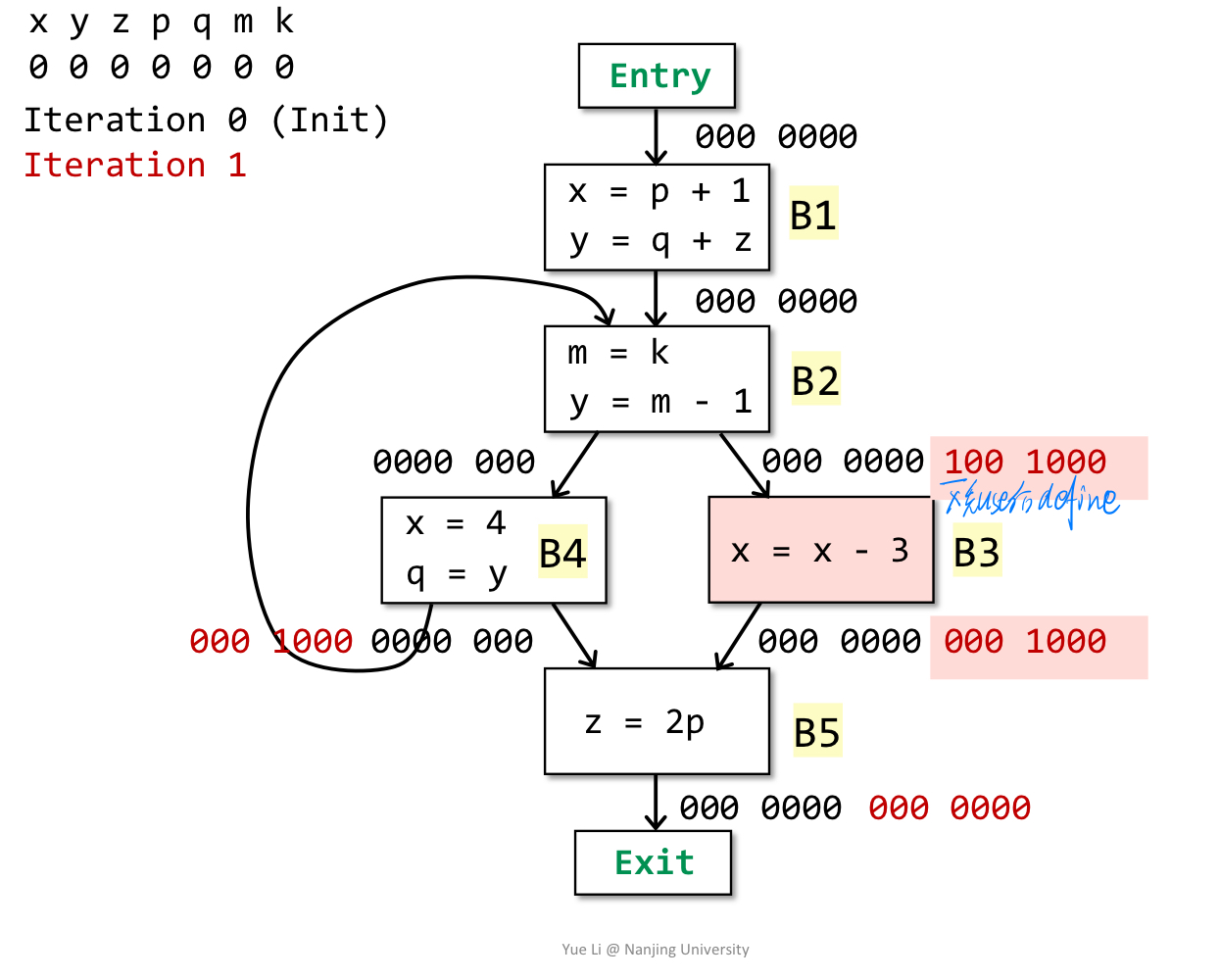
说明：算法初始化所有BB的in为全0，自下而上的迭代分析。此时需要分析B3的in，out为B5的in即0001000，use为B3自身涉及的x（注意这个表达式x=x-3，此时x为先use后def，故而仍然算是use并且def为0000000）即1000000，故而in为1000000 U (0001000 - 0000000) = 1001000。

活跃变量算法例子2

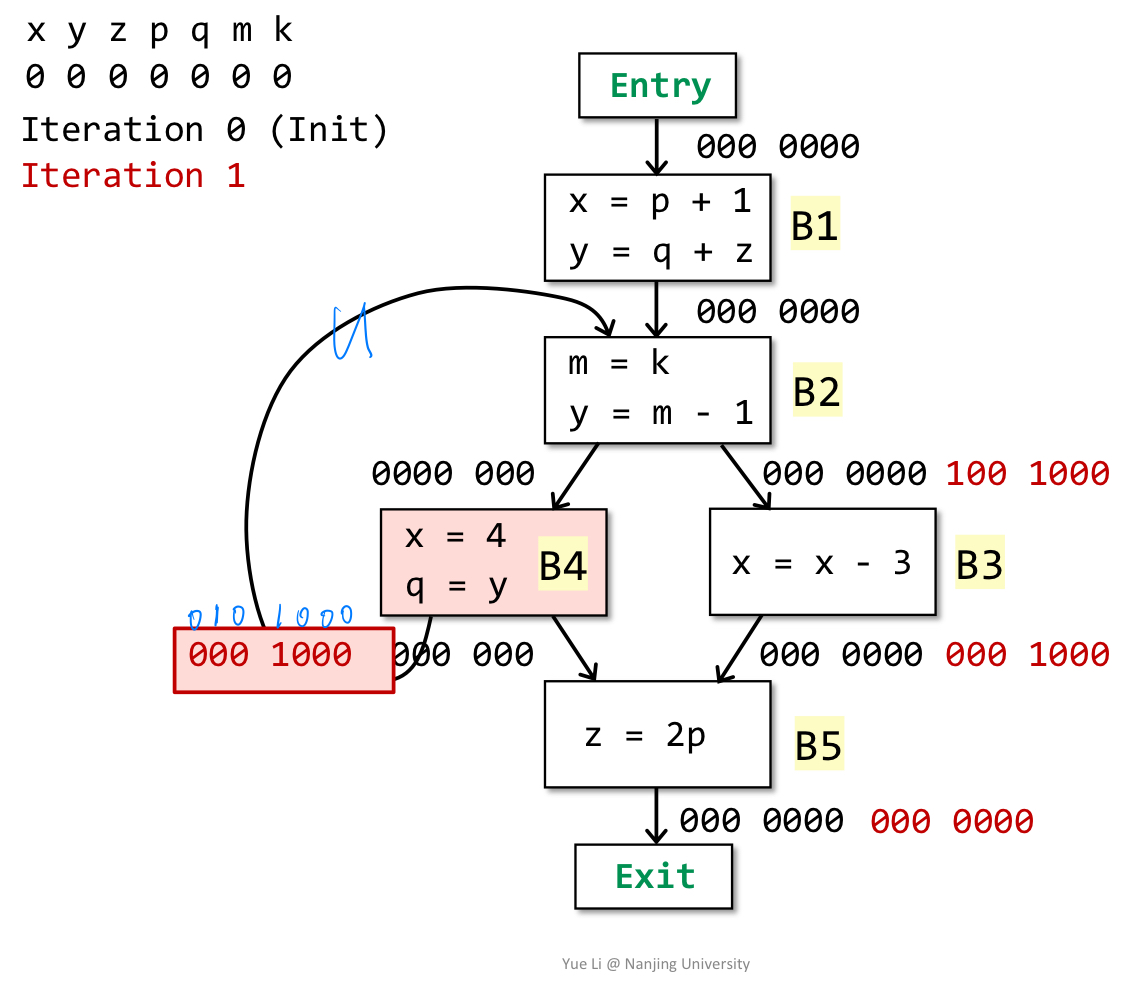
说明：此时分析B4的in，注意到B4的out有两个，需要先union，0001000（B5的in）U 0000000（初始值）= 0001000，use为B4涉及的y即0100000，def为x即1000000，故而in为0100000 U (0001000 - 1000000) = 0101000。

活跃变量算法例子3

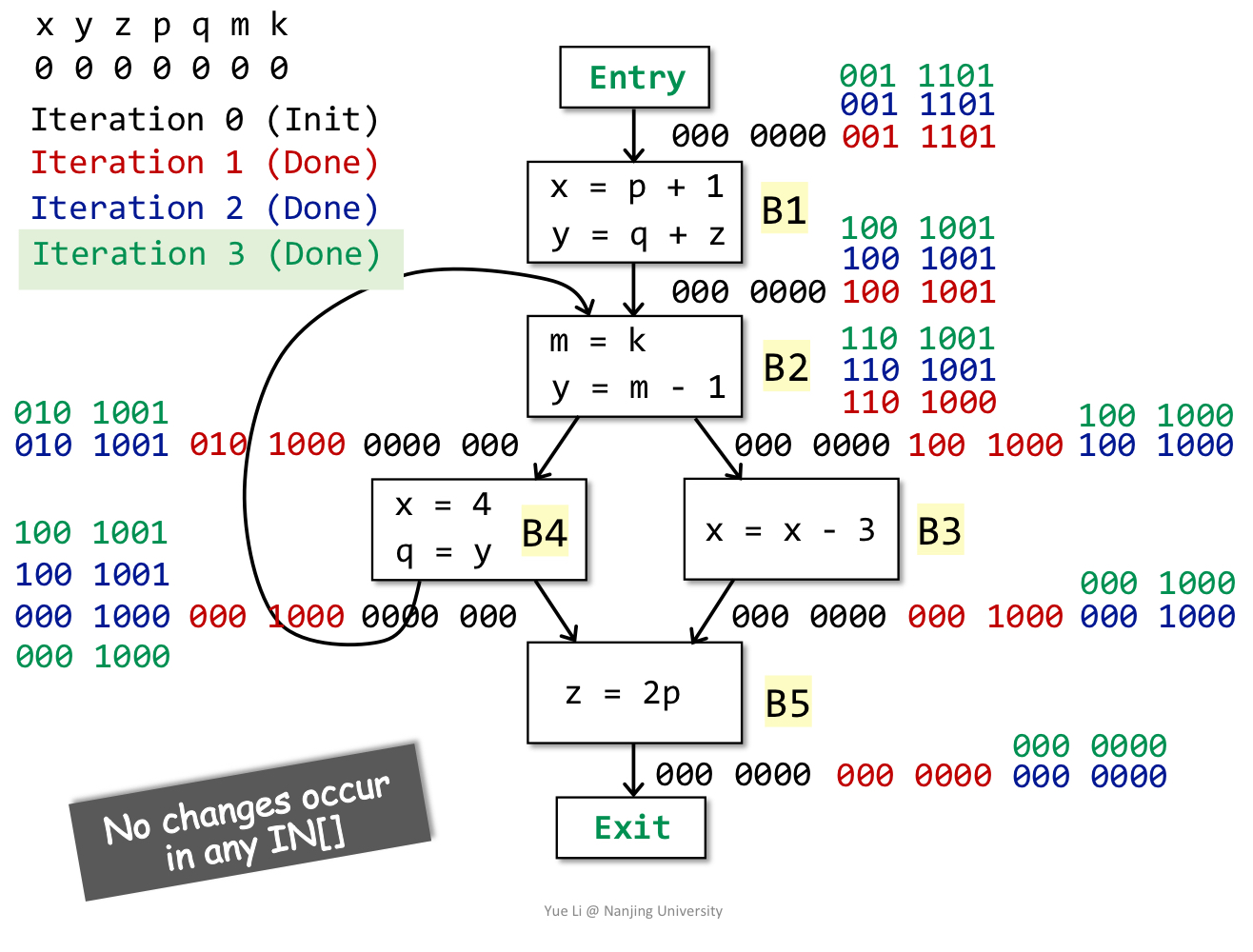
说明：经过3轮迭代计算，所有BB的in都没有改变，算法结束。

Available Expression Analysis 可用表达式分析

定义

An expression x op y is a available at program point p if (1) all paths from the entry to p must pass through the evaluation of x op y, and (2) after the last evaluation of x op y, there is no redefinition of x op y.

x + y 在 p 点可用的条件：从流图入口结点到达 p 的每条路径都对 x + y 求了值，且在最后一次求值之后再没有对 x 或 y 赋值

可用表达式可以用于全局公共子表达式的计算。也就是说，如果一个表达式上次计算的值到这次仍然可用，我们就能直接利用其中值，而不用进行再次的计算。

可用表达式分析中的数据流值

• 程序中的所有表达式
• bit vector 中，一个 bit 就是一个表达式

可用表达式的转移方程和控制流处理

可用表达式的转移方程和控制流处理

• 我们要求无论从哪条路径到达 B，表达式都应该已经计算，才能将其视为可用表达式，因此这是一个 must analysis。
• 注意到图中，两条不同的路径可能会导致表达式的结果最终不一致。但是我们只关心它的值能不能够再被重复利用，因此可以认为表达式可用。
• v = x op y，则 gen x op y。当 x = a op b，则任何包含 x 的表达式都被 kill 掉。若 gen 和 kill 同时存在，那么以最后一个操作为准。
• 转移方程很好理解，和到达定值差不多。但是，由于我们是 must analysis，因此控制流处理是取交集，而非到达定值那样取并集。
• 注意gen和kill的顺序，先kill后gen还是gen。

可用表达式的算法

可用表达式的算法

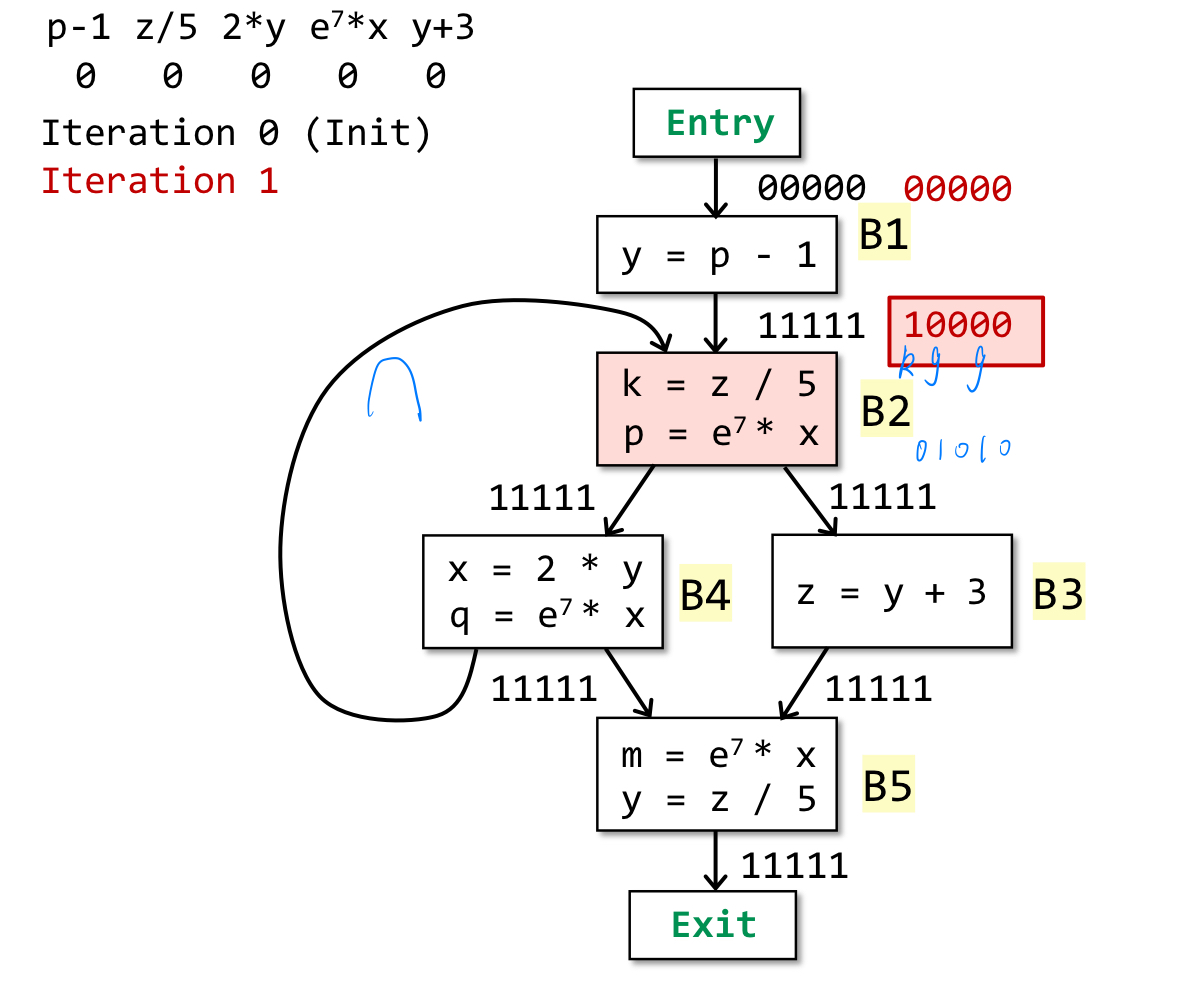
• 注意此时的初始化：一开始确实无任何表达式可用，因此OUT[entry]被初始化为空集是自然的。但是，其它基本块的 OUT 被初始化为全集，这是因为当 CFG 存在环时，一个空的初始化值，会让取交集阶段直接把第一次迭代的 IN 设置成 0，无法进行正确的判定了。
• 如果一个表达式从来都不可用，那么OUT[entry]的全 0 值会通过交操作将其置为 0，因此不用担心初始化为全 1 会否导致算法不正确。
• 计算抽象说明就是在out上将gen的改为1，kill的改为0。

可用表达式的算法例子1

说明：初始化entry处的out为全0，其他为全1。此时需要分析B2的out，注意到B2的in有两部分，取两部分的交集即10000，gen为B2自身涉及的z/5、e^7*x即01010，kill为B2涉及的p即10000，故而out为01010 U (10000 - 10000) = 01010。

可用表达式的算法例子2

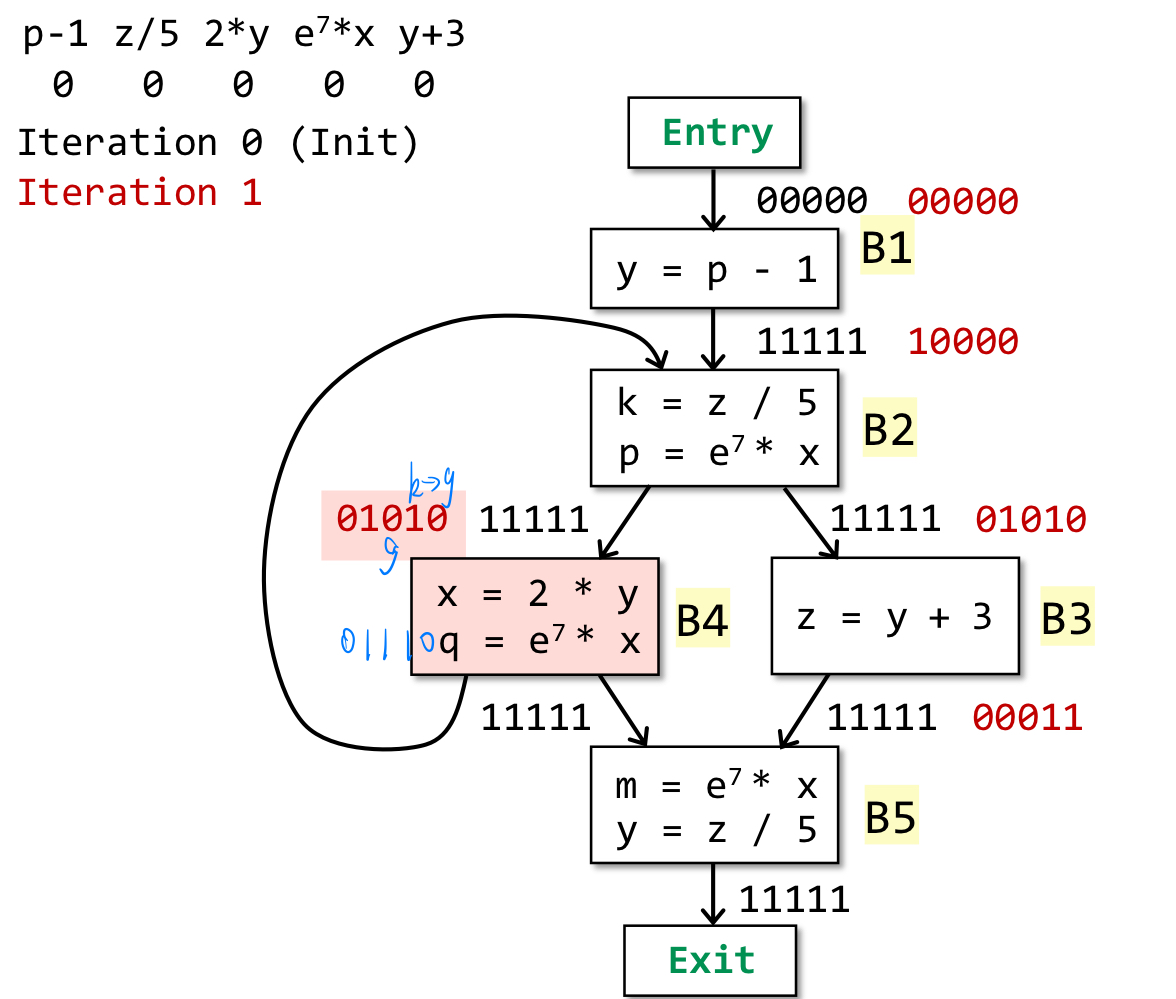
说明：此时分析B4的out，in为B2的out即01010，gen为B4自身涉及的2*y、e^7*x(注意这里是先kill后gen)即00110，kill为00000，故而out为01010 U (00110 - 00000) = 01110。

可用表达式的算法例子3

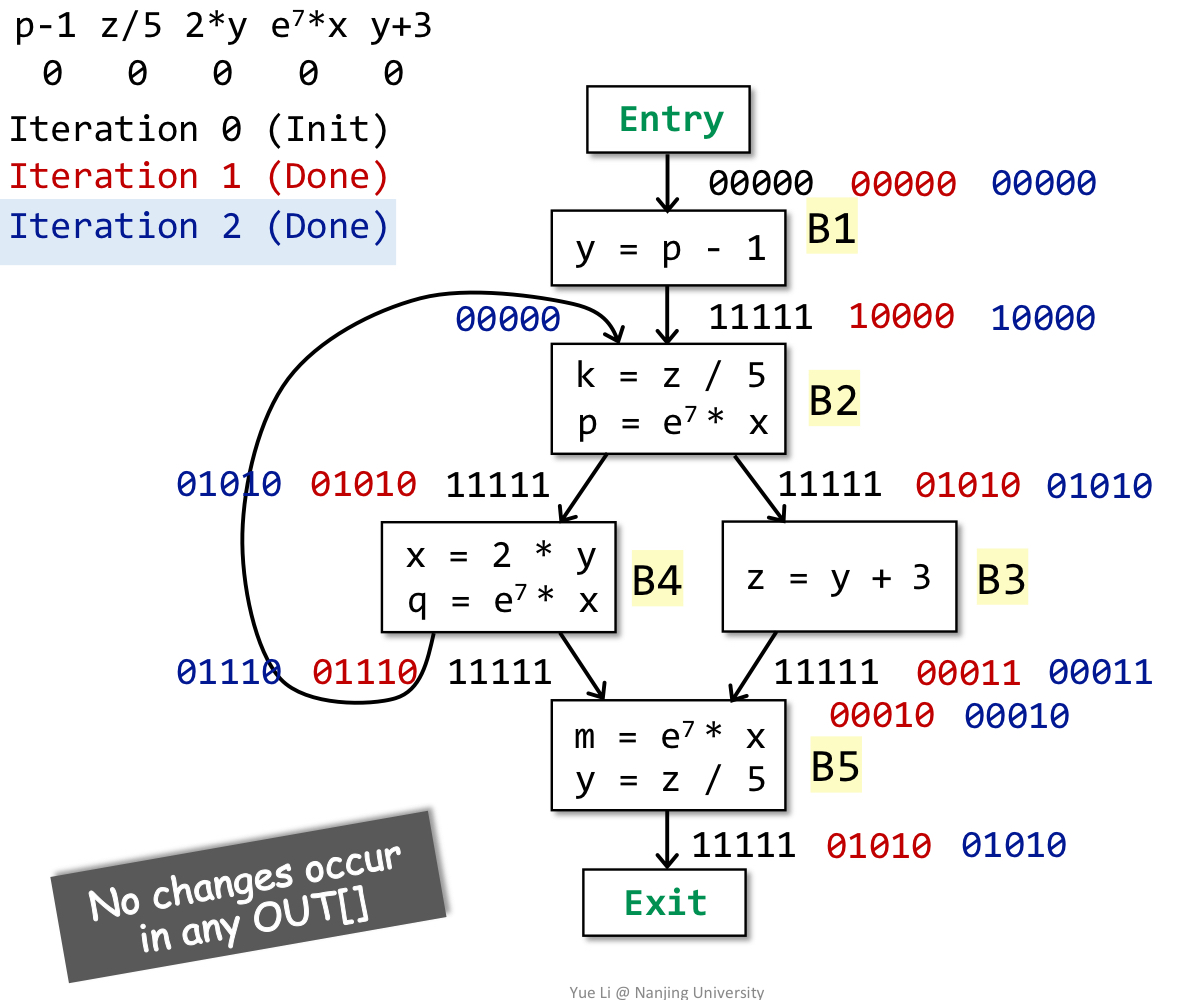
说明：经过2轮迭代计算，所有BB的out都没有改变，算法结束。

三种数据流分析总结

三种数据流分析总结对比

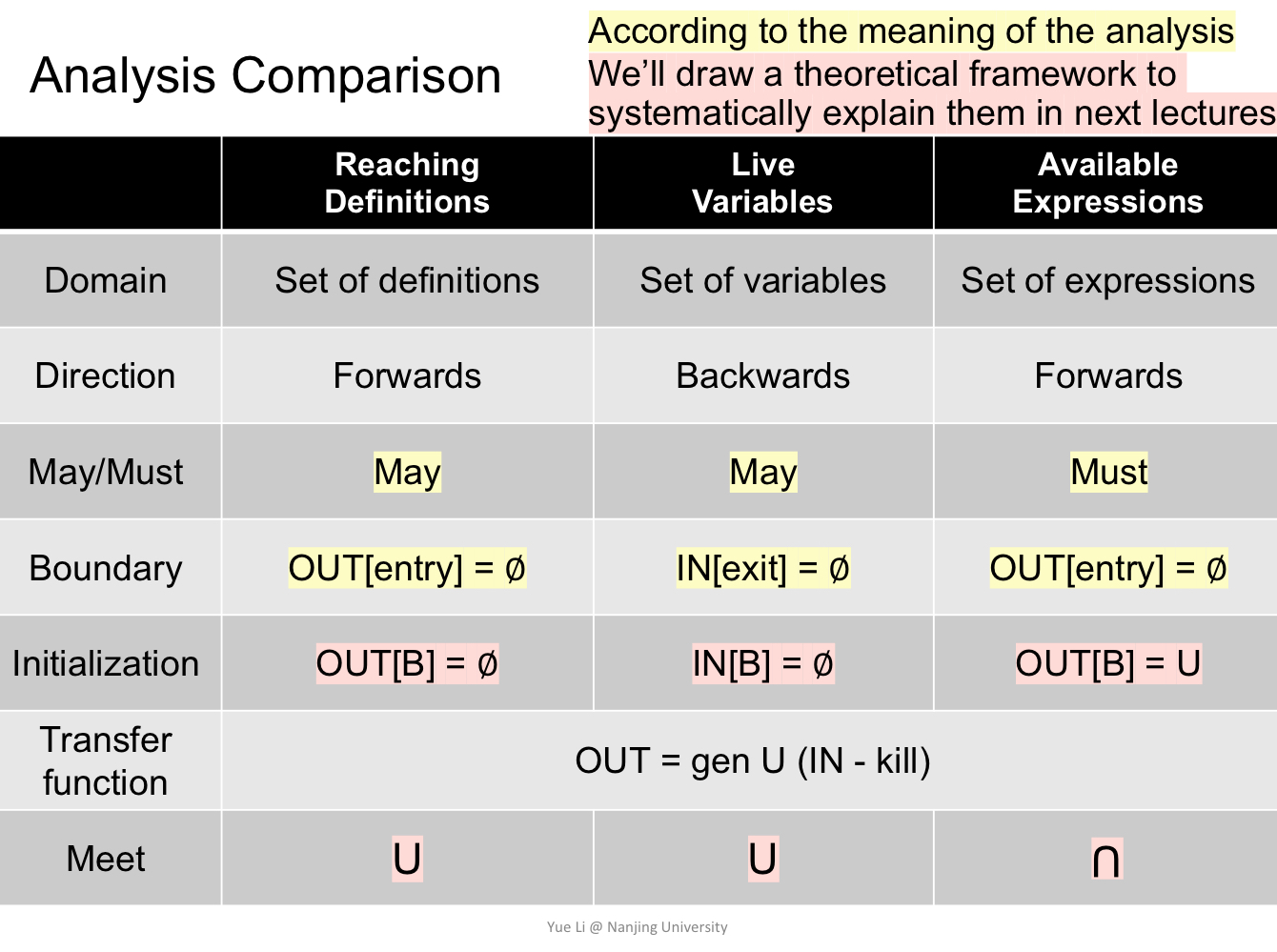
分析目标

• Reaching Definitions（到达定义分析）： 分析程序中每个基本块的定义信息（哪些变量的定义可以从前面流入当前块）。
• Live Variables（活跃变量分析）： 分析程序中每个基本块的活跃变量（哪些变量的值在未来可能被使用，需保留其定义）。
• Available Expressions（可用表达式分析）： 分析程序中每个基本块的表达式信息（哪些表达式在当前块之前已经计算且未被修改，可以直接复用）。

分析方向

• Reaching Definitions：前向分析（Forwards） 从程序的入口点向后传播，计算哪些定义到达了当前基本块。
• Live Variables：后向分析（Backwards） 从程序的出口点向前传播，计算哪些变量在未来的基本块中会被使用。
• Available Expressions：前向分析（Forwards） 从程序的入口点向后传播，计算哪些表达式在当前块可以直接复用。

May / Must 属性

• Reaching Definitions：May Analysis
  • 关心“某些定义可能到达当前块”。
  • 结果是所有可能的定义（宽松的上界）。
• Live Variables：May Analysis
  • 关心“某些变量可能在未来使用”。
  • 结果是所有可能活跃的变量（宽松的上界）。
• Available Expressions：Must Analysis
  • 关心“某些表达式必须在当前块可用”。
  • 结果是所有必须可用的表达式（严格的下界）。

边界条件（Boundary Condition）

• Reaching Definitions：
  • （入口点没有到达的定义）。
• Live Variables：
  • （程序出口没有活跃变量，因为没有后续的使用）。
• Available Expressions：
  • （入口点没有可用表达式）。

初始化（Initialization）

• Reaching Definitions:
  • 初始化 （默认没有到达的定义）。
• Live Variables:
  • 初始化 （默认没有活跃变量）。
• Available Expressions:
  • 初始化 （所有表达式都被假定为可用，直到证伪）。

传递函数（Transfer Function）

• 所有分析都基于以下公式的传递规则：

  • ：表示在当前基本块中生成的新信息。
  • ：表示在当前基本块中被覆盖或无效的信息。

合并操作（Meet Operation）

• Reaching Definitions 和 Live Variables： 合并操作是并集（Union），即所有可能到达或活跃的信息的集合。
• Available Expressions： 合并操作是交集（Intersection），即所有路径上共同可用的表达式。

总结

特性	Reaching Definitions	Live Variables	Available Expressions
目标	变量定义到达情况	变量活跃情况	可用表达式情况
分析方向	前向（Forwards）	后向（Backwards）	前向（Forwards）
May / Must	May	May	Must
边界条件
初始化
传递函数		同左	同左
合并操作	并集（Union）	并集（Union）	交集（Intersection）

每种分析都为程序优化提供不同的信息：

• Reaching Definitions 支持常量传播、死代码消除等。
• Live Variables 支持寄存器分配、内存优化。
• Available Expressions 支持公共子表达式消除等优化。

参考

南京大学《软件分析》课程 03 （Data Flow Analysis I） - 哔哩哔哩

南京大学《软件分析》课程 04 （Data Flow Analysis II） - 哔哩哔哩

数据流分析上 | Static Program Analysis Book (gitbook.io)