DFA-FD
Iterative Algorithm, Another View
给定一个有 k 个节点的 CFG,迭代算法会更新每个节点 n 的 OUT[n] 值。那么就可以考虑把这些值定义为一个 k-tuple:
则,我们的数据流分析迭代算法框架就可记为
迭代过程就被记为:
...
此时我们发现
,意味着 就是 的一个不动点。 在这个框架下,我们就有一些想知道的问题: Is the algorithm guaranteed to terminate or reach the fixed point, or does it always have a solution?
If so, is there only one solution or only one fixed point? If more than one, is our solution the best one (most precise)?
When will the algorithm reach the fixed point, or when can wo get the solution?
即:
- 算法是否确保一定能停止/达到不动点?会不会总是有一个解答?
- 如果能到达不动点,那么是不是只有一个不动点?如果有多个不动点,我们的结果是最优的吗?
- 什么时候我们会能得到不动点?
Partial Order
所谓偏序集合(poset),就是一个由集合
- Reflexivity 自反性:x
x - Antisymmetry 反对称性:x
y, y x, 则 x = y - Transitivity 传递性:x
y, y z, 则 x z - 例子:小于等于关系就是一个偏序关系,但小于关系不是偏序关系,它是全序关系。
偏序关系与全序关系的区别在于,全序关系可以让任意两个元素比较,而偏序关系不保证所有元素都能进行比较。
Upper and Lower Bounds
对于偏序集中的某子集 S 来说:
- 若存在元素 u 使得 S 的任意元素 x 有 x
u,那么我们说 u 是 S 的上界(Upper bound)。 - 同理,若存在元素 l 使得 S 的任意元素 x 有 l
x,那么我们说 l 是 S 的下界(Lower bound)。
然后我们衍生出最小上界和最大下界的概念:
- 在 S 的所有上界中,我们记最小上界(Least upper bound, lub)为
,满足所有上界 u 对 lub 有: - 类似地我们也能定义出最大下界(Greatest lower bound, glb)为
。

当 S 的元素个数只有两个{a, b}时,我们还可以有另一种记法:
- 最小上界:
, a join b - 最大下界:
, a meet b
并不是每个偏序集都有 lub 和 glb,但是如果有,那么该 lub, glb 将是唯一的。(可假设存在多个,然后用自反性证明它们是同一个:假设有两个lub,那其中一个按照定义应该是最小的,那两者中存在一个更小的,和原始定义冲突,故而只能是两者相同即唯一)

Lattice, Semilattice, Complete and Product Lattic
给定一个偏序集,如果任意元素 a, b 都有 lub和glb,那么这么偏序集就叫做 格(lattice)。
- 属于 lattice 的:小于等于关系,子集关系
- 不属于 lattice 的:子串关系
如果偏序集任意两元素的上下界仅有其 lub 和 glb,那么称该偏序集为半格(Semilattice)
如果在此之上更加严格一些,任意集合都存在 lub 和 glb,那么我们说这个 lattice 为 全格(complete lattice)
- 属于全格的:子集关系
- 不属于全格的:小于等于关系,因为全体正整数没有一个边界
每一个全格都存在着最大元素
如果一个 lattice 是有穷的,那么它一定是一个全格。然而,一个全格不一定是有穷的,例如[0, 1]之间的实数是无穷的,但是期间的小于等于关系可以使其成为全格。
另外还有 Product Lattice,多个 lattice 的笛卡尔积也能形成一个新的 lattice。
需要记住的是:
- product lattice 也是一个 lattice
- 如果 product lattice L是全格的积,那么 L 也是全格。
Example 1. Is
Example 2.Is
Example 3.Is
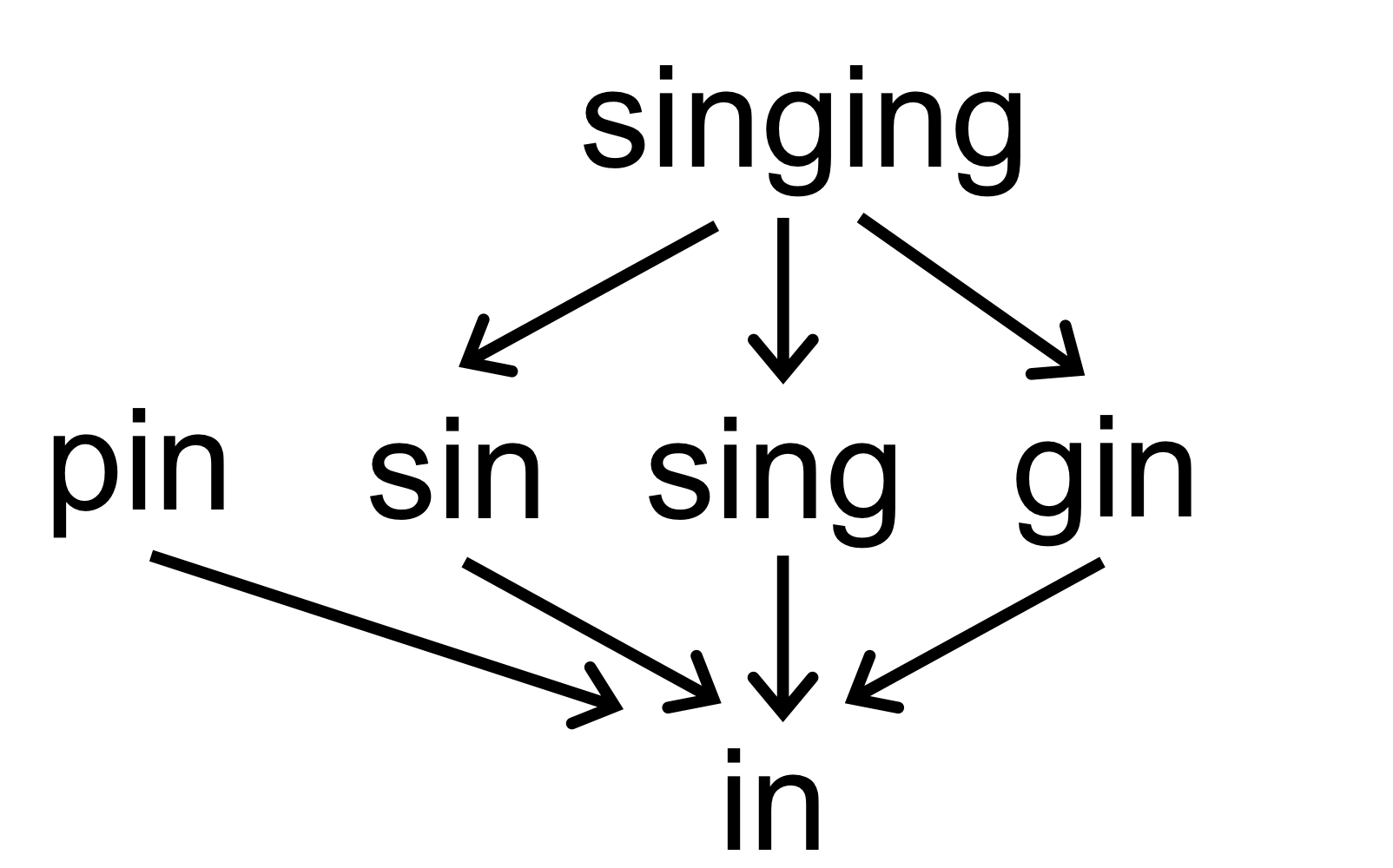
Example 4. Is
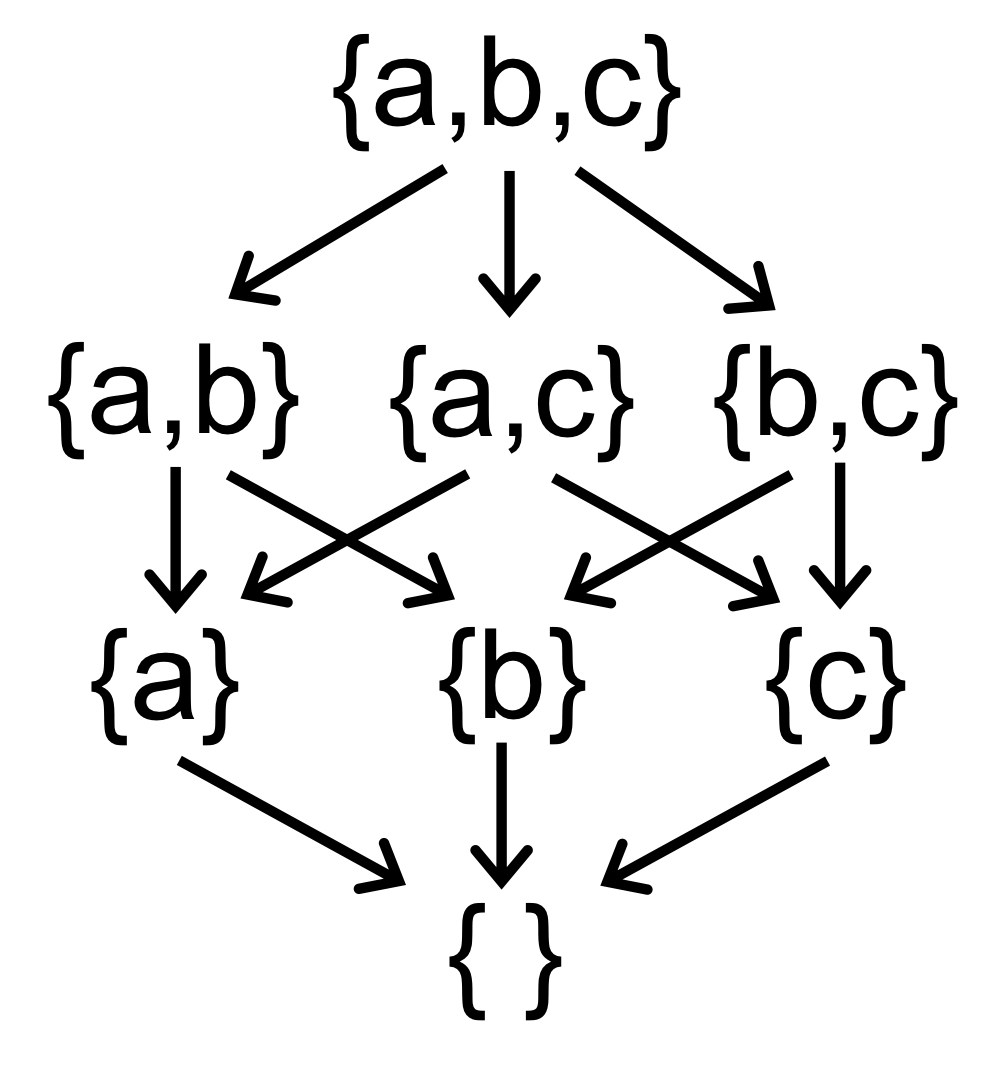
| example | 偏序 | 格 | 全格 |
|---|---|---|---|
| 1 | 属于 | 属于 | 无上界,无穷,不属于全格 |
| 2 | 不满足自反性 | ||
| 3 | 属于 | 不属于 | |
| 4 | 属于 | 属于 | 属于 |
Data Flow Analysis Framework via Lattice
一个数据流分析框架(D, L, F)由以下元素组成:
- D: 数据流的方向,前向还是后向
- L: 包含了数据值 V 和 meet, join 符号的格(一般选其一,也就是半格)
- F: V -> V 的转移方程族
从而,数据流分析可以被视为在 lattice 的值上迭代地应用转移方程和 meet/join 操作符。
Monotonicity and Fixed Point Theorem
回看我们在上面提出的问题:迭代算法在什么条件下可以停止?我们在这里引入不动点定理:
Monotonicity 单调性:如果
FIxed Point Theorem 不动点定理:给定一个全格
是单调的 是有穷的
也就是f单调有界+L全格,那么
- 迭代
可以得到最小不动点(least fixed point) - 迭代
可以得到最大不动点(greatest fixed point)
证明:
根据
由于 L 是有限的,且 f 单调,根据鸽笼原理,必然存在一个 k 使得$f() f2()...fk()f^{k+1}()
假设我们有另一个任意不动点 x,由于 f 是单调的,因此
可知的确
通过上面的证明,我们又回答了一个问题:如果我们的迭代算法符合不动点定理的要求,那么迭代得到的不动点,确实就是最优不动点。


Relate Iterative Algorithm to Fixed Point Theorem
以上我们只是定性的描述了是否能得到最优不动点,但是迭代算法怎样才能算是符合了不动点定理的要求呢?接下来介绍关联的方法。
首先,回想 fact 的形式:
然后,我们的迭代函数 F 包括了转移函数 f 和 join/meet 函数,证明 F 是单调的,那么也就能得到
这里分两部分。
- 转移函数,即
,显然是单调的。 - 那么 join/meet 函数,我们要证明其单调,就是要证明:
,有 。 - 由定义,
- 由传递性,
- 则
是 的 lub - 又
是 的 lub - 因此
,证毕。
- 由定义,
于是我们就完成了迭代算法到不动点定理的对应。
现在我们要回答本文开头的第三个问题了,什么时候算法停止?
这个问题就很简单了,因为每个 lattice 都有其高度。假设 lattice 的高度为 h,而我们的 CFG 节点数为 k,就算每次迭代可以使一个节点在 lattice 上升一个高度,那么最坏情况下,我们的迭代次数也就是
最后我们再列出这三个问题与其回答:
- 算法是否确保一定能停止/达到不动点?能!会不会总是有一个解答?可以!
- 如果能到达不动点,那么是不是只有一个不动点?可以有很多。如果有多个不动点,我们的结果是最优的吗?是的!
- 什么时候我们会能得到不动点?最坏情况下,是 lattice 的高度与 CFG 的节点数的乘积。
May/Must Analysis, A Lattice View
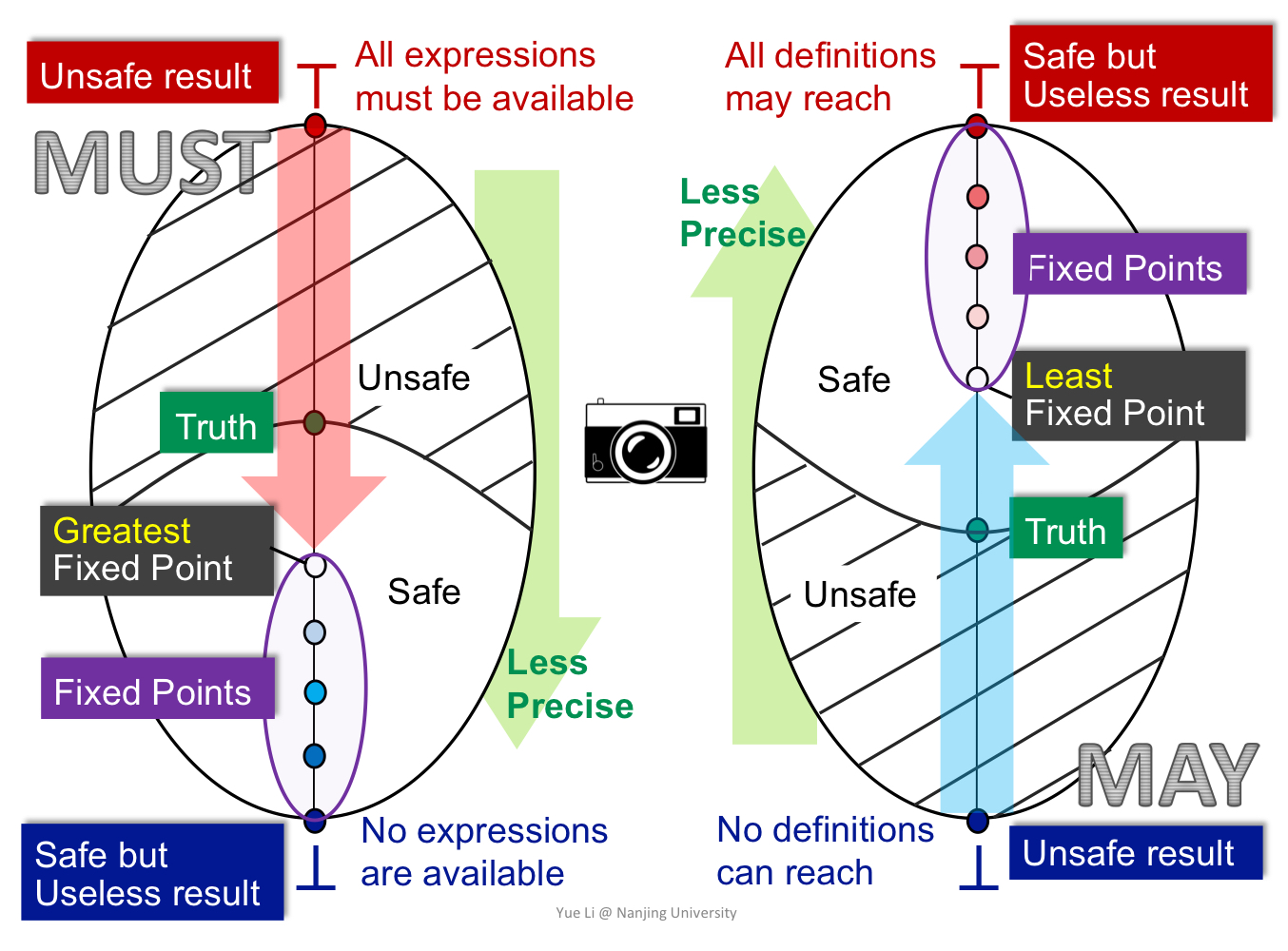
无论 may 还是 must 分析,都是从一个方向到另一个方向去走。考虑我们的 lattice 抽象成这样一个视图。
例如,对于到达定值分析,下界代表没有任何可到达的定值,上界代表所有定值都可到达。
下界代表 unsafe 的情形,即我们认为无到达定值,可对相关变量的存储空间进行替换。上界代表 safe but useless 的情形,即认为定值必然到达,但是这对我们寻找一个可替换掉的存储空间毫无意义。
而因为我们采用了 join 函数,那么我们必然会从 lattice 的最小下界往上走。而越往上走,我们就会失去更多的精确值。那么,在所有不动点中我们寻找最小不动点,那么就能得到精确值最大的结果。
反之,在可用表达式分析中,下界代表无可用表达式,上界代表所有表达式都可用。
下界代表 safe but useless 的情形,因为需要重新计算每个表达式,即使确实有表达式可用。而上界代表 unsafe,因为不是所有路径都能使表达式都可用。与 may analysis 一样,通过寻找最大不动点,我们能得到合法的结果中精确值最大的结果。
Distributivity and MOP
我们引入 Meet-Over-All-Paths Solution,即 MOP。在这个 solution 中,我们不是根据节点与其前驱/后继节点的关系来迭代计算数据流,而是直接查找所有路径,根据所有路径的计算结果再取上/下界。这个结果是最理想的结果。
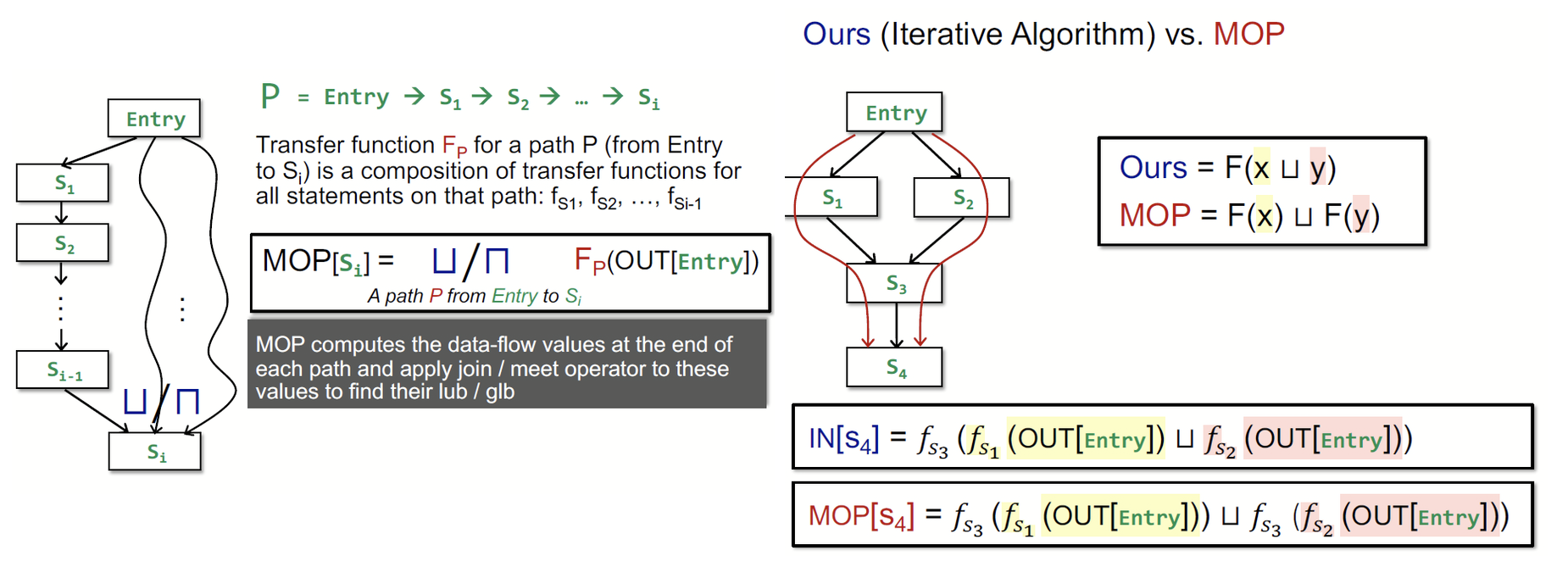
可以看到,迭代算法是 s3 对前驱取 join 后进行进行 f3 的转移,而 MOP 算法是对到达 s3 之后,s4 之前的路径结果取 join。
那么迭代算法和 MOP 哪个更精确呢?我们可以证明,

这表明 MOP 是更为精确的。
但这并没有结束。而如果 F 是可分配的,那么确实可以让偏序符号改为等于号。恰好,gen/kill problem 下,F 确实可分配因此我们能确定,迭代算法的精度与 MOP 相等。
Constant Propagation
当然有些问题下 F 是不可分配的,如常量传播(Constant Propagation)。
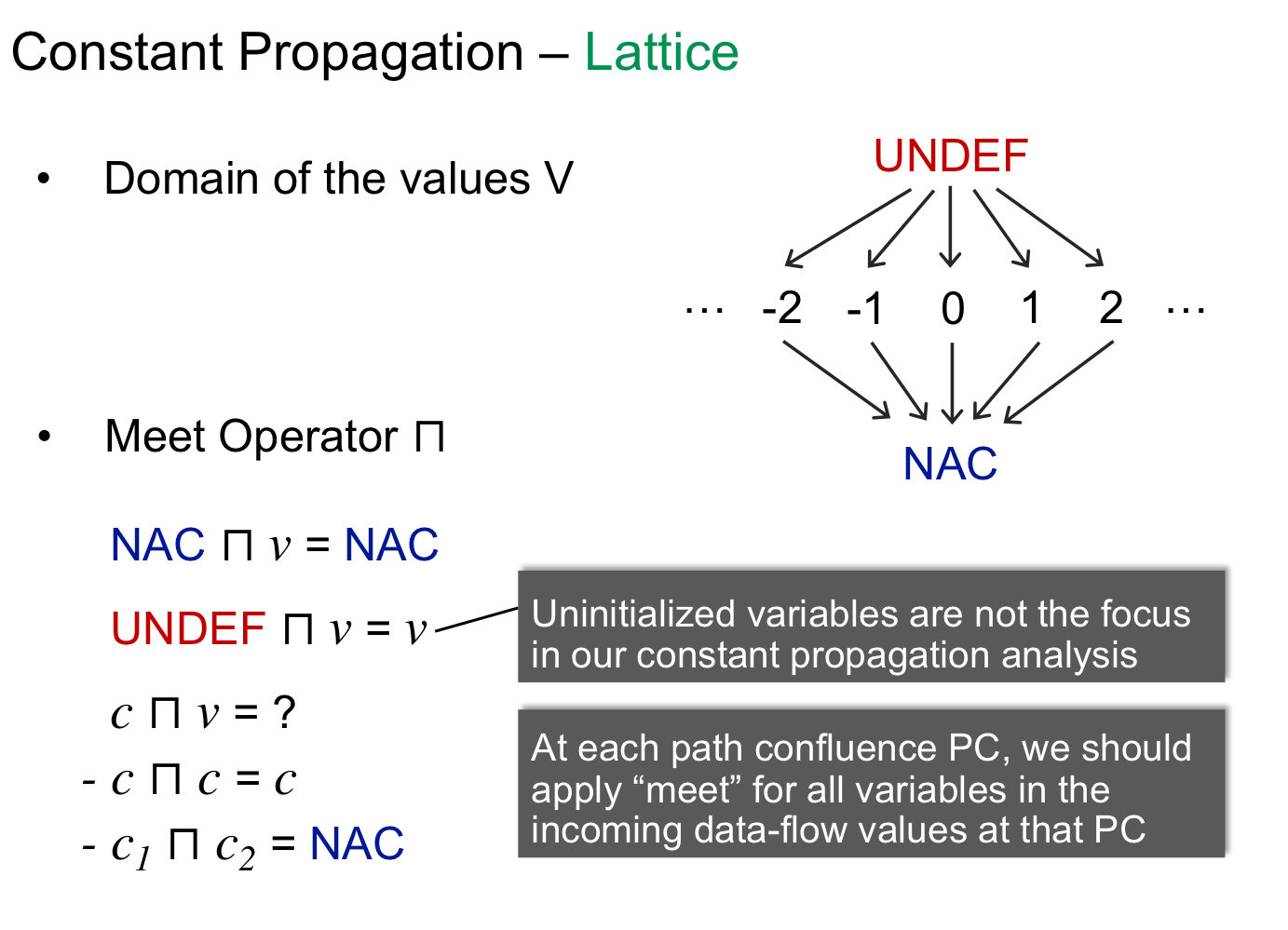
在常量传播分析中,其最大上界是 undefine,因为我们不知道一个变量到底被定义为了什么值。最小下界是 NAC(Not A Constant),而中间就是各种常量。这是因为分析一个变量指向的值是否为常量,那么要么它是同一个值,要么它不是常量。
给定一个 statement s: x = ...,我们定义转移函数
其中我们根据赋值号右边的不同,决定不同的 gen 函数:

注意,const + undef -> undef。因为 undef 变成 const 的过程中是降级,而如果 const1 + undef -> const2,那么 undef 变化为 const 时,const2 会发生改变,原来的 const2 与现在的 const2 不具有偏序关系,那么就不满足偏序关系的单调性了。
常量传播是不可分配的。以下图为例:对于 c,
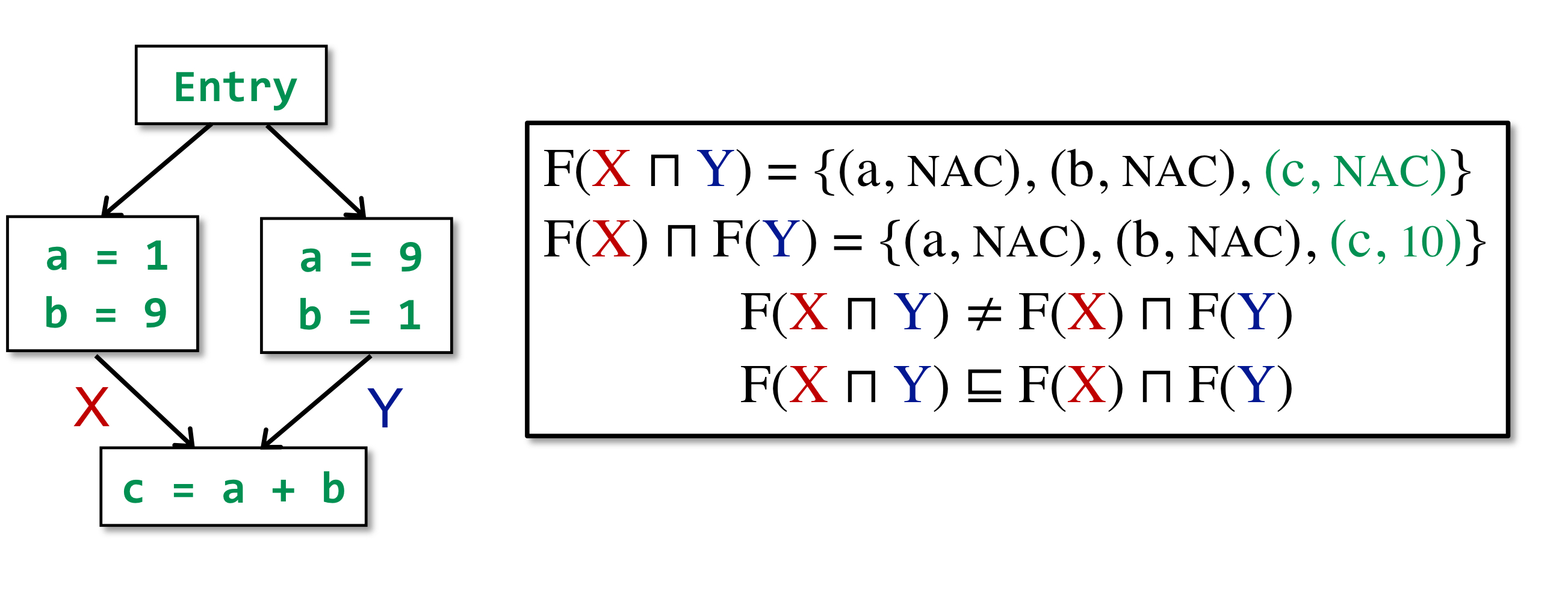
Worklist Algorithm
在 Worklist 算法中,只在基本块的 fact 发生变化处理其相关基本块,不必再在每次有 fact 变化时处理所有的基本块了。原来算法的优化,比较简单。

划重点
- 理解函数视角下的迭代算法
- 对于 lattice 和 complete lattice 的定义
- 理解不动点定理
- 知道如何用 lattice 来概述 may 和 must analysis
- MOP与迭代算法结果之间的关系
- 常量传播分析
- Worklist 算法
参考
南京大学《软件分析》课程 05 (Data Flow Analysis - Foundations I) - 哔哩哔哩
南京大学《软件分析》课程 06 (Data Flow Analysis - Foundations II) - 哔哩哔哩